深入理解ResNet

ResNet能够work的主要原因:

• 作者说残差结构是为了解决网络退化的问题，作者猜测

We conjecture that the deep plain nets may have exponentially low convergence rates, which impact the reducing of the training error. The reason for such optimization difficulties will be studied in the future.

认为 deep plain nets 可能有指数级低收敛率，限制了训练误差的进一步降低。他简单地比较了残差结构和常规结构在求解本征映射(identity map)时的优化难度，显然求解 F(x)=0 比求解 H(x) = x 容易得多
也就是说能够更好地学习到差分特征，相当更容易学习到残差的那一部分。(这是ResNet有效地最主要原因)

残差网络对数据波动更敏感

我们回到设计 ResNet 的初衷： 为了解决深度网络的 退化 问题 。该问题的直接表现形式为： 深度网络在的训练误差比浅层网络高，无法做到使深层网络在训练数据集上“ 过拟合 ”。那么如何做到“过拟合”呢？ 答案就是我们需要使网络对数据波动更敏感，尽可能地去准确描述数据。而残差网络就是这样的一种网络结构。
假设某几层 layer 要学习的函数 H(x) 如紫线所示，红色点表示采样点，对应一个数据样本。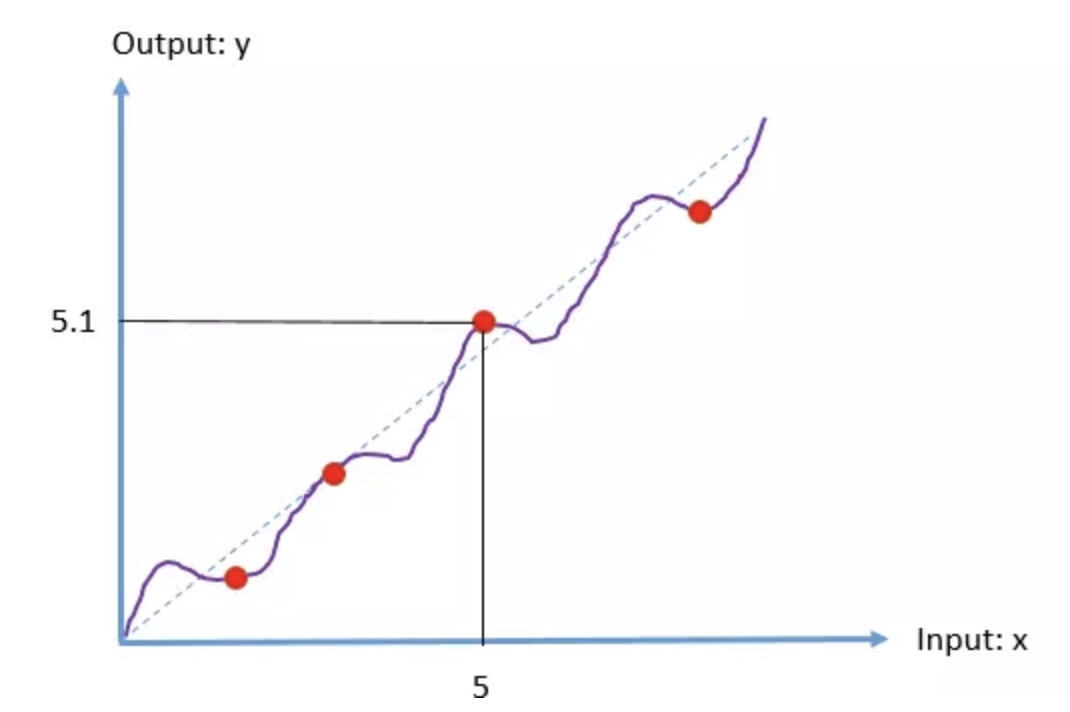

在ResNet 中激活函数全部采用 ReLU， 我们知道 采用 ReLU 的网络是局部空间的线性网络的组合。
对于数据点（5,5.1），即我们的 input 为5， 期望输出为5.1，假设为 plain network， 我们在 x =5 的附近，学习到的线性参数值为 w = 5.1/5 , 若数据点变成（5,5.2），我们仍可以用 w= 5.1/5 的线性网络近似，因为此时网络输出 5.1 与理想值 5.2 只相差 2% 而已. 所以在 plain net 中，网络对 数据不敏感。
数据的波动指的是相对对角线 y= x 的波动, 残差网络的思想是：我们用 y= x 先去粗略拟合数据， “波动”也即“拟合残差”就交给 weight layer 去拟合。数据点（5,5.1）对应的残差为（5,0.1），此时假设学习到的参数为 w=0.1/5 。同样地，若数据点变成（5,5.2），对应的残差为（5,0.2）。显然地，我们不可以用 0.1/5 近似了，因为若用0.1/5 近似，网络输出 0.1 和 0.2 相差了100%。网络需要调整 w 的值，以尽可能精确地描述残差。所以综上所述，残差网络对数据变得敏感，也即对“数据波动更敏感”，更容易做到“过拟合”。

• 集成学习思想，ResNet是由很多条路径集成学习得到的，对于每个block如果残差为0就退化为直连。如果所有resblock的残差都是0，那么就退化成VGG网络。
• 特征表示，跳层连接使得表达特征更加丰富，比如说前面网络层的浅层特征能够和深层的特征融合。2017年的DenseNet网络有类似的设计。
• 缓解梯度消失问题，梯度能够直接传到skip connection前面的网络层（不是主要原因，作者说这个梯度消失的问题使用Batch Normalization就能解决，但resNet确实有缓解梯度消失的效果）
  

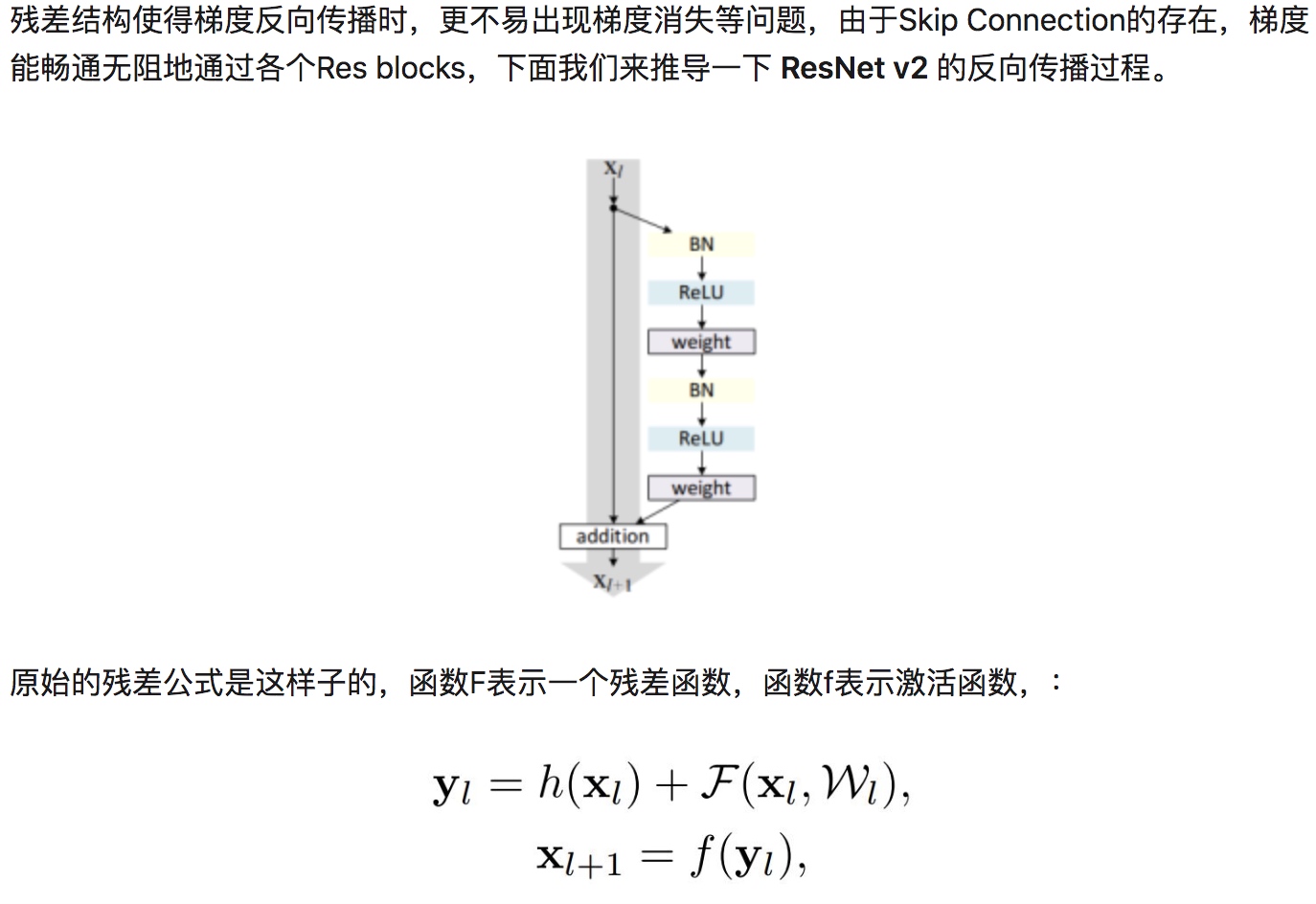
参考

https://zhuanlan.zhihu.com/p/54289848
https://www.jianshu.com/p/ca6bee9eb888